Following this post on Aragon. My thought on how to implement liquid voting.
Definitions
First let’s define the variable we will use to compute complexity of a voting round.
n: The amount of accounts.
d: The amount of delegation/undelegation in this round.
r: The amount of accounts required for the proposal to win. For example imagine there is 1 “No” voter with 80 votes, 10 “Yes” voters (either directly or through delegation) with 1 vote each and 1000 “Yes” voters with 1 vote each, we have n=1011 but r=9 (since 9 “Yes” voters with 10 votes are sufficient to get more “Yes” votes than “No” votes). Account may be required due to their votes or because they get delegations.
a: The amount of active accounts (those who vote directly, not through a delegation).
We are interested by the following complexities:
Off-Chain Delegation complexity The off-chain complexity of updating the delegations, this includes undelegations.
On-Chain Delegation complexity The on-chain complexity of updating the delegations, this includes undelegations.
Off-Chain resolution complexity The off-chain complexity of operations which must be done in order for the vote result to be correct.
On-Chain resolution complexity The on-chain complexity of operations which must be done in order for the vote result to be correct.
Aragon Topic Proposal
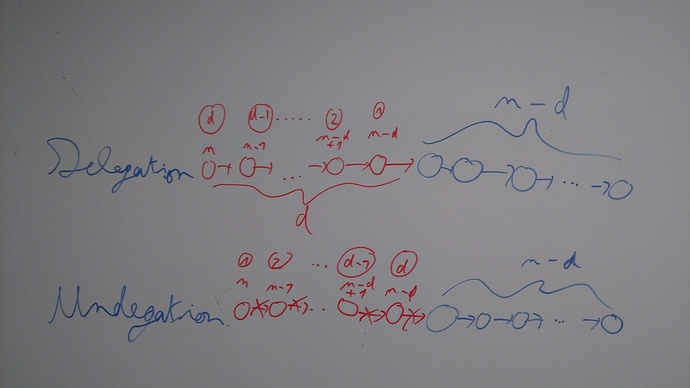
In topic implementation, in the worst case delegations form a chain and are added in order.
Assuming that the chain has n-d accounts which already did their delegation, there is d delegations remaining.
The first delegation will take n-d, the second n-d+1, … the last n on-chain time.
So the total on-chain delegation complexity will be O(d*(n+(n-d)/2))=O(d*n).
Off chain, there is nothing particular to do.
For undelegation in, the worst case, they are done in reverse order which lead to the same complexity.
The first undelegation will take n, the second n-1, … the last n-d on-chain time.
Worst case scenario
So we have
Off-Chain Delegation complexity=O(d)
On-Chain Delegation complexity=O(d * n)
To find the result, we just have to sum the votes of the final delegates which vote the proposal.
Off-Chain resolution complexity=O(a)
On-Chain resolution complexity=O(a)
So the resolution is really efficient, but the undelegation is really problematic as O(d * n) is not practical.
Implementation without tracking the sum of delegations
We propose to make a trade off and increase the resolution complexity in order to decrease the delegation complexity.
Delegation just links the account to the delegate and undelegation remove this link.
So each delegation/undelegation is in O(1) which leads to
Off-Chain Delegation complexity=O(d)
On-Chain Delegation complexity=O(d)
But now, the problem is getting the sum of the votes, we can trivially do so in O(n) by doing a any kind of traversal (depth-first or breadth-first) and summing the values of the encountered nodes.
Note that the problem of the gas limit can easily be solved by allowing multiple transactions to finish the vote (see the IICO contract for an example: openiico-contract/contracts/IICO.sol at master · kleros/openiico-contract · GitHub).
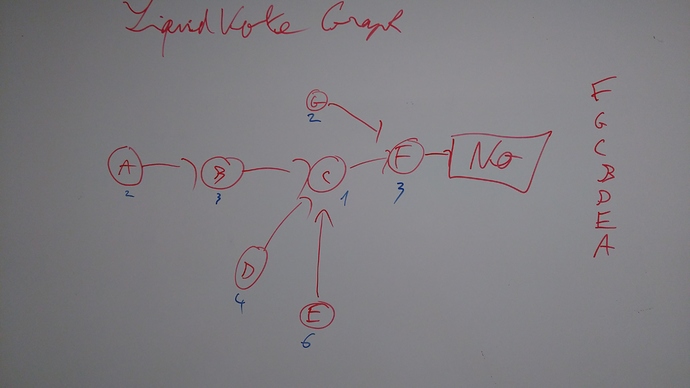
Delegation Graph
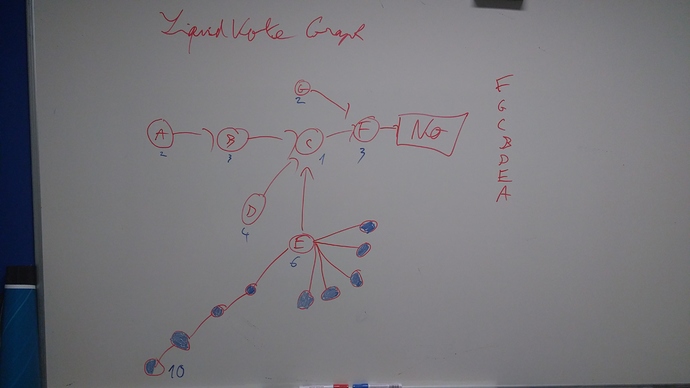
However, this in not satisfactory as someone could split his tokens into numerous accounts which would have a O(m) cost and lead to a O(m) grief in each vote. So a O(v) griefing factor where v is the amount of votes after the attack.
Fully colored nodes are attacking duplicate accounts with a negligible amount of voting rights, the partially colored one is an attacking one with a non negligible amount of voting rights.
On-Chain resolution complexity=O(r)
Off-Chain resolution complexity=?
Research Directions
Period reactivations
A way to lower the griefing potential would be to require delegations to be reactivated periodically.
Gas subsidies
A way to remove this griefing opportunity would be to require account making delegation to give a deposit which would cover the gas cost of the parties calling the resolution function. This deposit would also need to be renew periodically.
Interactive Verification
We could do an off-chain traversal of the graph an put the result. We would let people challenge the result using a procedure similar to Truebit (https://truebit.io/).
Only relevant on-chain computations
Another solution would be to keep on-chain complexity minimal by only “showing to the blockchain” the relevant nodes, this can be achieved by only showing the r accounts which are required for a proposal to win. The caller would provide a partial traversal of the graph of the winning proposal (eventually in multiple TXs) which would allow to get on-chain a lower bound of the amount of votes for a proposal.
Anyone would be able to do so for every proposal.
After some time, the proposal with the higher lower bound would be considered the winning one. Since it is always possible to show a lower bound of the winning proposal which exceed the amount of vote of other proposal, if someone is dedicated to have the winning proposal win, it would.
On-chain computations would only need to cover r, the minimum amount of account required for the proposal to win and we would have On-Chain resolution complexity=O(r) which is practical.
If an attacker were to make extra accounts in order to increase the computational cost and those accounts were required for the proposal to win, it could effectively increase r. But this is not a problem as in this case, it means that the attacker could swing the vote which would be worse for proponent of the proposal compared to an increase of the resolution cost (as proponent of the proposal can always choose not to pay the resolution cost, letting the another proposal win).
However, we would need to determine off-chain the minimum set of accounts to display a lower bound of the votes on the winning proposal greater than the votes of the second proposal. At this point I haven’t been able to find a polynomial procedure to do so (but I haven’t searched that much…). Even if no polynomial/practical procedure were to be found, we could use heuristics, but those heuristics would need to be resistant to attackers.
A possible heuristic would be to find the “cutoff” value by dichotomic search and remove from the graph all of the accounts having less votes than the “cutoff” value.
The dichotomic search could be done off chain and the partial traversal (which would not consider nodes with less votes than the cutoff value) could be done on-chain, removing the need to enumerate the required nodes when calling the contract handling the vote.